
It is saved as a hash table which contains the generating rays and the basis of the lineality space of the cone as well as the defining half-spaces and hyperplanes. +mkn+1) give a secant projective space to the veronese curve, and one can compute the dual space of this secant and it is the intersection of the (mi)-1. the current polyhedron is intersected with an additional halfspace that defines P.
#CHECK IF HYPERPLAN INTERSECTS ORTHANT FULL#
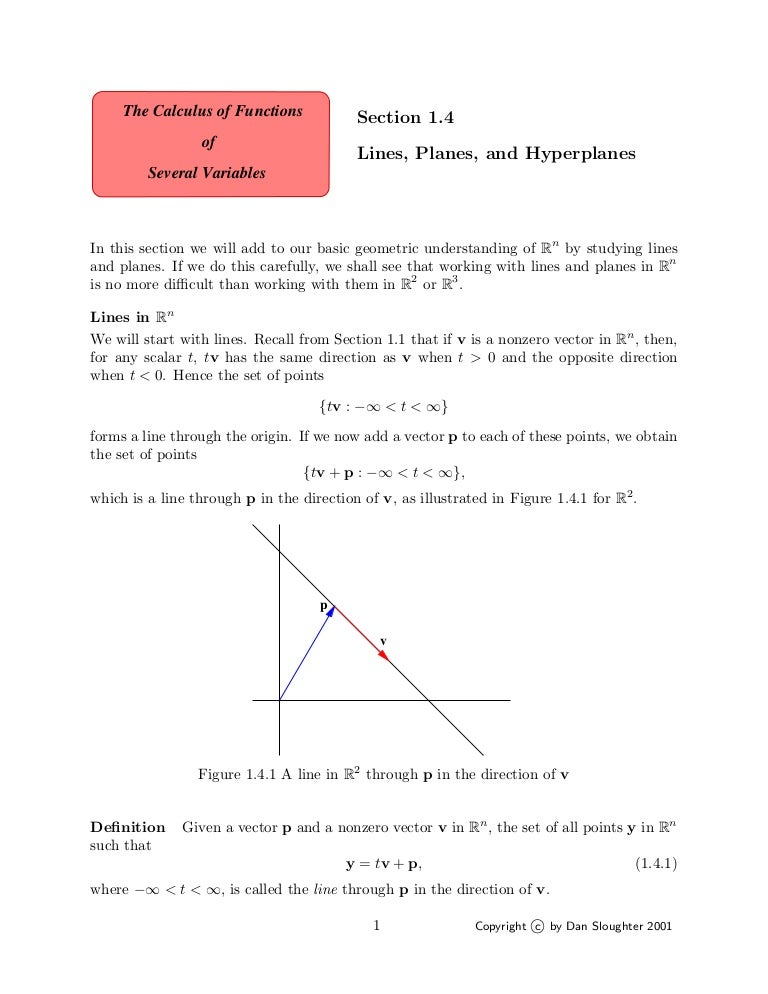
It need not be full dimensional or may contain a proper linear subspace.
#CHECK IF HYPERPLAN INTERSECTS ORTHANT DOWNLOAD#
For an introduction to higher dimensional polytopes see 14, and for a description of the double description method and its variants, consult 2. Diagrammatic Analysis of Interval Linear Equations -Part II: The Two-Dimensional Case and Generalization to n Dimensions Zenon Kulpa download BookSC. line2 (numpy.array): slope, intercept of the second line.

If it does not contain any vertex of P, it must intersect the interior of P and separate at least one pair of vertices of P. If it contains any vertex of P, it is visited by T. Args: line1 (numpy.array): slope, intercept of the first line. Let P be a convex polytope that intersects every hyperplane of I, and T be any tour on the vertices of P. def getintersection (line1, line2): '''Returns the intersection, if any, between two lines, None if the lines are equal, and the empty array if the lines are parallel. A Cone represents a rational convex polyhedral cone. The non-negative orthant Rn is the collection of vectors x Rn with x 0, that is, vectors whose coordinates are non-negative numbers. Repeat the process for each of your line segments.


 0 kommentar(er)
0 kommentar(er)
